Selection and dose adjustment

In fig. temporary dynamics of therapeutic effect at single administration of drug is presented. The therapeutic effect is shown after introduction after a while, gradually reaches a maximum, then weakens and eventually disappears. Dynamics of therapeutic effect corresponds to changes of serumal concentration of drug which are defined by its pharmacokinetic features (an absorption, distribution, elimination). The therapeutic effect appears on reaching therapeutic concentration and increases in process of its augmentation. Duration of effect depends on time during which serumal concentration exceeds therapeutic. Similarly side effects depend on toxic concentration of drug. In the range between these concentration (therapeutic range) medicine is effective, but has no side effect. At repeated administration of drug the dose and an interval between introductions are selected so that to reach the maximum therapeutic effect at the minimum side effect. As a rule, take serumal concentration in which the therapeutic effect makes about a half from maximum for the lower bound of therapeutic range. The top border corresponds to concentration in which side effects arise no more than at 5 — 10% of patients. Toxic concentration of some medicines exceeds therapeutic less than twice. It is necessary to remember also specific features of patients: one well transfer the serumal concentration exceeding toxic, and at others the expressed side effects arise when serumal concentration remains within therapeutic range.

If it is easy to estimate pharmacological effects of medicine (for example, on change of the ABP or level of a glucose of plasma), then the dose can be selected a trial and error method. To define in what limits and it is how often possible to change a dose, use the empirical rules considering the pharmacokinetic patterns given above (for example, the dose is changed no more than for 50% and aren't more often than through 3 — 4T1/2). If there is no toxicity, for ensuring maximum efficiency and augmentation of time of effect of drug it is possible to give a dose much above average therapeutic. For example, act with Penicillinums and the majority of β-adrenoblockers this way..........

If it is difficult to estimate pharmacological effects, medicine has narrow therapeutic range, is high risk of a side effect and inefficiency of treatment or drug use with the preventive purpose, the dose is changed slightly, carefully watching the patient for identification of side effects. Anyway, average concentration of medicine in steady state has to be in limits of therapeutic range. In most cases to define the actual serumal concentration of drug there is no need: there is enough only approximately the nobility as she depends on a dose and the frequency of introduction. However for a small number of drugs therapeutic concentration differs from toxic by only 2 — 3 times (digoxin, Theophyllinum, lidocaine, aminoglycosides, cyclosporine, anticonvulsants). In this case when calculating a dose proceed from the required average concentration of drug (usually in plasma) in steady state in which it is effective, but gives a minimum of side effects. Then measure the actual concentration of drug and if necessary correct a dose so that the actual concentration was as it is possible closer to demanded (see also hl. 3).

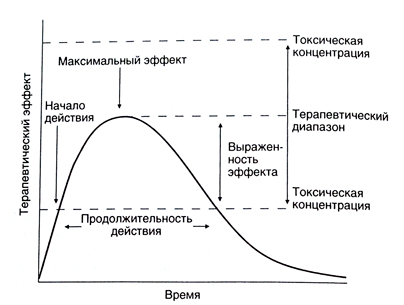
The description to fig. Temporary dynamics of therapeutic effect at single administration of medicine. The therapeutic effect is shown only after concentration of drug exceeds therapeutic. Then the effect increases (in process of a further absorption and distribution of drug) and reaches a maximum then gradually weakens as a result of elimination of drug and disappears as soon as serumal concentration falls below therapeutic again. Duration of therapeutic effect depends on time during which serumal concentration of drug remains higher than therapeutic. If concentration exceeds toxic, the probability of side effects increases. Therefore, serumal concentration needs to be maintained in limits between therapeutic and toxic, that is within therapeutic range. In such concentration medicine is effective, but almost doesn't give side effects. At augmentation or a dose decline the therapeutic effect respectively amplifies or weakens (the curve of dependence of therapeutic effect of time is displaced down or up). At augmentation of a dose also duration of effect of drug is enlarged. However it is possible to extend action in such a way only when therapeutic range is rather wide (for example, at Penicillinums) as at augmentation of a dose also the risk of side effects increases. For maintenance of serumal concentration within the therapeutic range and ensuring continuous effect of drug use repeated introduction.

Maintenance dose

In most cases medicine is entered fractionally or in the form of infusion so that stationary concentration was in limits of therapeutic range. Rate of entering of drug is peer steady state to rate of its elimination (the equation 1.1, 1.14). Having substituted in the equation 1.14 the required serumal concentration of drug, we will receive:

Rate of entering = Ssredn x Cl/F (1.16)

Knowing the required serumal concentration of drug, its clearance and bioavailability, it is possible to calculate a dose and frequency of introduction. You can try Pinealon.

Example. The patient with a heart failure weighing 69 kg accepts digoxin in maintenance doses. The required average serumal concentration of digoxin in steady state makes 1.5 ng/ml. SKF is peer to 100 ml/min. Using the equation given in the Appendix II it is possible to calculate digoxin clearance:

Cl = 0,88 x SKF + 0,33 ml/min. = 0,88 x 100/69 + 0,33 ml/min. — 1,6 ml/min. =110 ml/min. = 6,6 l/h.

The dose and frequency of reception (that is rate of entering of drug) can be calculated on the basis of the equation 1.16. Bioavailability of digoxin is peer to 0.7.

Rate of entering = Ssredn x Cl/F = 1.5 ng/ml x x 1.6/0.7 ml/min. = 3.43 ng/kg / min. = 236 ng / min. = 236 x 60 x 24 mkg/days = 340 mkg/days = 0.34 mg/days.

In practice the dose is rounded to the next standard, for example to 375 mg/days or to 0.25 mg/days. In the first case average concentration in plasma in steady state will make 1.5x375/340 = 1.65 ng/ml, in the second — 1.5 x 250/340 = 1.1 ng/ml.

Interval between introductions

It is desirable that in an interval between introductions there were no sharp fluctuations of serumal concentration of drug. If the absorption and distribution of drug occurred instantly, scope of these fluctuations would depend only on T1/2-When the interval between introductions is peer to T1/2, the minimum and maximum concentration differ twice that is quite admissible.

If the therapeutic range of medicine is rather wide, that is in the concentration considerably exceeding therapeutic, it is transferred well, it is possible to prescribe the maximum doses. In that case the interval between introductions can be much more T 1/2 that is very convenient for the patient. Amoxicillin T1/2, for example, makes about 2 h, but drug is usually prescribed in high doses at an interval of 8 — 12 h.

For medicines with a narrow therapeutic range quite often it is necessary to measure the maximum and minimum serumal concentration. The minimum concentration in steady state is counted on the following equation:

Smin = (F x Dose/Vß) / (1-e-kT) x e-kT (1.17)

where k = 0,693/T1/2, and T — an interval between introductions. Size e-kT represents the share of the previous dose which remained in an organism by the time of introduction of the following dose (taking into account bioavailability).

If dynamics of concentration of medicine for intake is described by several exponential functions, for calculation of the maximum concentration in steady state it is necessary to know a series of the constants characterizing an absorption and distribution of drug. If e-kT in numerator of the equation 1.17 and these constants to neglect size, at multiple dose the maximum concentration in steady state can be calculated on the equation 1.18 (see below). However because of the specified allowances settlement concentration will be higher than real.

Example. In the example reviewed above the maintenance dose of digoxin for the patient with a heart failure was calculated. At reception of 0,375 mg/days average serumal concentration of digoxin in steady state will make 1.65 ng/ml. As the therapeutic range of digoxin is narrow (0.8 — 2 ng/ml), it is necessary to calculate the minimum and maximum serumal concentration of drug in intervals between receptions. At first on the equation given in the Appendix II we will calculate the volume of distribution of digoxin in steady state:

Vc = 3,12 x SKF +3,84l/kg = 3,12 x (100/69) + 3,84 l/kg = 8,4 l/kg = 580 l weighing 69 kg.

Knowing Vc and a clearance of digoxin, it is possible to calculate T1/2 (the equations 1.1 — 1.12):

T1/2=0,693 xVc/Cl = 0,693 x 580l/6.6 l/h = 61 h

The constant of speed of elimination is equal to 0,693/61, that is 0,01136 h'. The maximum and minimum concentration of digoxin depend on an interval between receptions. Calculation of these concentration at medicine reception each 2 days is given below.

Smax = (Fkhdoza/Vs) / (1-e-kT) = (0,7 x 0,375 h2 mg / 580ë)/0.42=2,15 ng/ml (1.18)

Smin = Relish x e-kT = 2,15 ng/ml x 0,58 = 1,25 ng/ml. (1.19)

So, at digoxin reception each 2 days the minimum and maximum concentration differ approximately twice (and has to be as the interval between receptions approximately corresponds to T1/2). But the maximum serumal concentration exceeds the upper bound of therapeutic range that increases risk of side effects, and minimum is only insignificant above the lower bound. If at the same dose to reduce an interval between receptions, fluctuations of serumal concentration will be significantly less, and average concentration won't change (1,65 ng/ml). At digoxin reception every day (0,375 mg/days) settlement maximum and minimum serumal concentration will make respectively 1,9 and 1,44 ng/ml. Both of these values are in the top part of therapeutic range. At reception of a smaller dose (0,25 mg/days) the maximum and minimum concentration are equal to 1,26 and 0,96 ng/ml, and average — 1,1 ng/ml. Choosing the scheme of treatment, it is necessary to compare probability of non-compliance with medical instructions (at frequent reception) and risk of side effects or inefficiency of treatment (at reception with long intervals).

Sating dose

Quicker to reach steady state, enter the sating dose (once or fractionally). She can be calculated as follows: The sating dose = Ssredn x Vc/F (1.20)

The sating dose is used in case steady state (and therapeutic effect) has to be reached quicker, than at introduction with constant rate, that is quicker than through 4T1/2. For Lidocainum, for example, the T 1/2 makes 1 — 2 h. Steady state, respectively, is reached in 4 — 8 h. At life-endangering arrhythmias against the background of a myocardial infarction it is impossible to wait so longly therefore in the block of an intensive care usually enter the sating Lidocainum dose. Introduction of the sating dose has the disadvantages.

First, the risk of side effects as serumal concentration of drug can exceed toxic increases. If T1/2 is rather big, too high concentration remains long enough. Secondly, the sating dose usually larger is also entered i.v. within a short period of time. It can be especially dangerous if drug has a side effect on intensively krovosnabzhayemy tissues in which equilibrium between concentration of substance in plasma and tissues quickly is established. The matter is that the sating dose is counted on distribution volume in steady state of Vc, but at first after introduction this dose can be distributed in much smaller volume. Therefore it is better to enter the sating dose fractionally, for rather wide interval of time, or by slow infusion. In the latter case it is desirable that rate of administering exponential decreased according to dynamics of accumulation of drug at introduction of maintenance doses. Now it is quite possible thanks to emergence of programmable infusional pumps. Example. In the example reviewed above (reception of digoxin in maintenance doses) achievement of steady state will require not less than 10 days (T)/2 = = 61 h). If it is necessary that steady state was established quicker (hl. 34), prescribe the sating dose. It is possible to calculate it on the equation 1.20:

The sating dose = 1.5 ng/ml x 580 l / 0.7 = 1243 mkg" 1 mg.

The sating dose can be accepted inside or to enter i.v. To reduce risk of side effects, it is split up. In the beginning enter 0.5 mg, in 6 — 8 h — 0.25 more mg, carefully watching the patient. The last 0,25 mg if necessary too can be divided into 2 doses on 0,125 mg and to enter them at an interval of 6 — 8 h, especially if to reception of digoxin in a maintenance dose it is planned to pass during 24 h from the moment of an initiation of treatment.

Individual selection of a dose

The scheme of treatment is defined on the basis of patterns of an absorption, distribution and elimination of drug and pharmacokinetic parameters (F, Cl, Vc and T1/2). The recommended schemes are usually designed for the "average" patient. Normal values of the major pharmacokinetic parameters of separate medicines and their change at different pathological and physiological states are given in the Appendix II. However these sizes are subject to appreciable unpredictable individual fluctuations. For many medicines the standard deviation of such parameters as F, S1 and Vc, makes respectively 20, 50 and 30%. In other words, in 95% of cases serumal concentration is in steady state ranging from 35 to 270% demanded that is unacceptable for drugs with a narrow therapeutic range. Therefore individual selection of a dose and frequency of introduction — the most important condition of efficiency of treatment. Based on the pharmacokinetic patterns described above, the scheme of treatment is selected so that to provide the necessary therapeutic effect and to minimize a side effect. Whenever possible measure serumal concentration of medicine. On the basis of the obtained data correct a dose of drugs with a narrow therapeutic range (for example, cardiac glycosides, antiarrhytmic and anticonvulsants, Theophyllinum).

Figure Temporary dynamics of therapeutic effect at single administration of medicine. The therapeutic effect is shown only after concentration of drug exceeds therapeutic. Then the effect increases (in process of a further absorption and distribution of drug) and reaches a maximum then gradually weakens as a result of elimination of drug and disappears as soon as serumal concentration falls below therapeutic again. Duration of therapeutic effect depends on time during which serumal concentration of drug remains higher than therapeutic. If concentration exceeds toxic, the probability of side effects increases. Therefore, serumal concentration needs to be maintained in limits between therapeutic and toxic, that is within therapeutic range. In such concentration medicine is effective, but almost doesn't give side effects. At augmentation or a dose decline the therapeutic effect respectively amplifies or weakens (the curve of dependence of therapeutic effect of time is displaced down or up). At augmentation of a dose also duration of effect of drug is enlarged. However it is possible to extend action in such a way only when therapeutic range is rather wide (for example, at Penicillinums) as at augmentation of a dose also the risk of side effects increases. For maintenance of serumal concentration within the therapeutic range and ensuring continuous effect of drug use repeated introduction.